To find the domain of a function, consider any restrictions on the input values that would make the function undefined, including dividing by zero, taking the square root of a negative number, or taking the logarithm of a negative number. Remove these values from the set of all possible input values to find the domain of the function.
Ex 1: Determine the Domain and Range of the Graph of a Function – YouTube
Answer: This is a radical function. The domain of a radical function is any x value for which the radicand (the value under the radical sign) is not negative. That means x+5\geq0 x+ 5 ≥ 0, so x\geq−5 x ≥ −5 . Since the square root must always be positive or 0 0, \displaystyle \sqrt x+5\ge 0 x+5 ≥ 0.

Source Image: study.com
Download Image
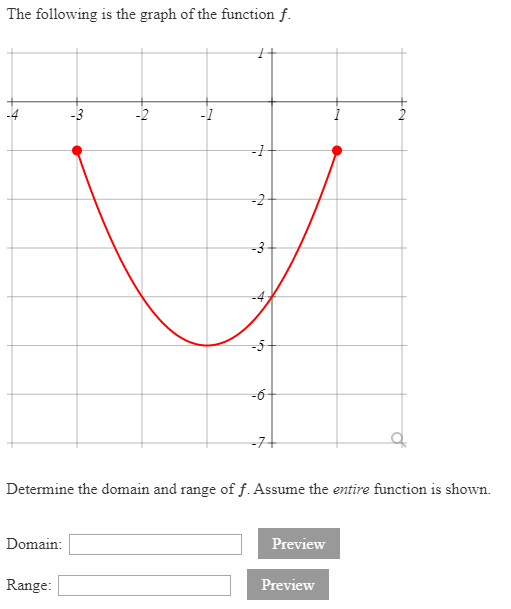
Solution We can observe that the horizontal extent of the graph is -3 to 1, so the domain of \displaystyle f f is \displaystyle \left (-3,1\right] (−3, 1]. Figure 8 The vertical extent of the graph is 0 to -4, so the range is \displaystyle \left [-4,0\right] [−4, 0]. Ex 1: Determine the Domain and Range of the Graph of a Function
Source Image: chegg.com
Download Image
Domain and Range of a Function
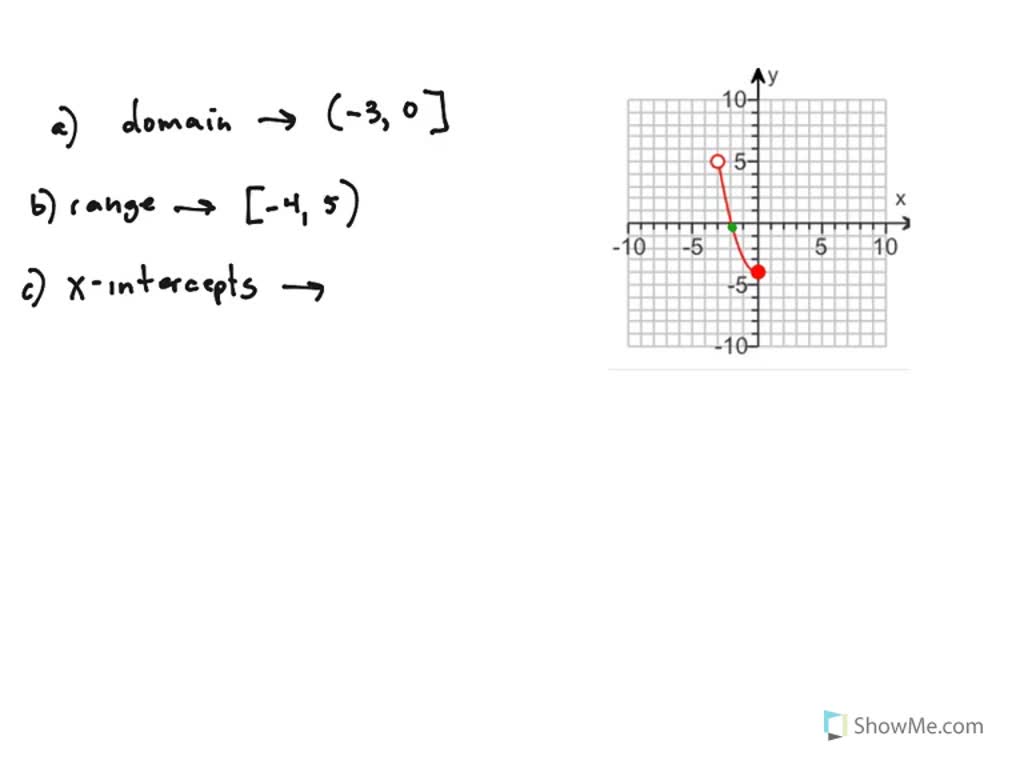
The graph is made up of three parts. The left part is defined for all values of x between – 4 and – 2. The part in the center is defined on the interval x > 0 and x ≤ 4. The part on the right is defined for x > 6 and x ≤ 6. The domain is written as a union of three intervals as follows.

Source Image: quizlet.com
Download Image
Determine The Domain_3 Of The Following Graph
The graph is made up of three parts. The left part is defined for all values of x between – 4 and – 2. The part in the center is defined on the interval x > 0 and x ≤ 4. The part on the right is defined for x > 6 and x ≤ 6. The domain is written as a union of three intervals as follows.
How To: Given the formula for a function, determine the domain and range. Exclude from the domain any input values that result in division by zero. Exclude from the domain any input values that have nonreal (or undefined) number outputs. Use the valid input values to determine the range of the output values.
CISSP Domain 3: Security Architecture and Engineering Diagram | Quizlet
Step 1: Enter the formula for which you want to calculate the domain and range. The Domain and Range Calculator finds all possible x and y values for a given function. Step 2: Click the blue arrow to submit. Choose “Find the Domain and Range” from the topic selector and click to see the result in our Calculus Calculator ! Examples
Which of the following best describes the domain and range of the relation in the graph? Domain: {1 < x – brainly.com

Source Image: brainly.com
Download Image
Teaching in Special Education: Domain and Range
Step 1: Enter the formula for which you want to calculate the domain and range. The Domain and Range Calculator finds all possible x and y values for a given function. Step 2: Click the blue arrow to submit. Choose “Find the Domain and Range” from the topic selector and click to see the result in our Calculus Calculator ! Examples

Source Image: teachinginspecialeducation.blogspot.com
Download Image
Ex 1: Determine the Domain and Range of the Graph of a Function – YouTube
To find the domain of a function, consider any restrictions on the input values that would make the function undefined, including dividing by zero, taking the square root of a negative number, or taking the logarithm of a negative number. Remove these values from the set of all possible input values to find the domain of the function.

Source Image: youtube.com
Download Image
Domain and Range of a Function
Solution We can observe that the horizontal extent of the graph is -3 to 1, so the domain of \displaystyle f f is \displaystyle \left (-3,1\right] (−3, 1]. Figure 8 The vertical extent of the graph is 0 to -4, so the range is \displaystyle \left [-4,0\right] [−4, 0]. Ex 1: Determine the Domain and Range of the Graph of a Function
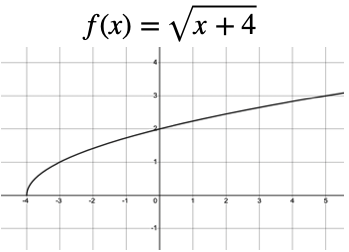
Source Image: intmath.com
Download Image
SOLVED: Use the graph to determine the following: 1. Find the function’s domain. (Type your answer in interval notation:) 2. Find the function’s range. (Type your answer in interval notation:) 3. Find
Identify Graphs of Basic Functions. We used the equation y = 2x − 3 y = 2 x − 3 and its graph as we developed the vertical line test. We said that the relation defined by the equation y = 2x − 3 y = 2 x − 3 is a function. We can write this as in function notation as f(x) = 2x − 3. f ( x) = 2 x − 3. It still means the same thing.
Source Image: numerade.com
Download Image
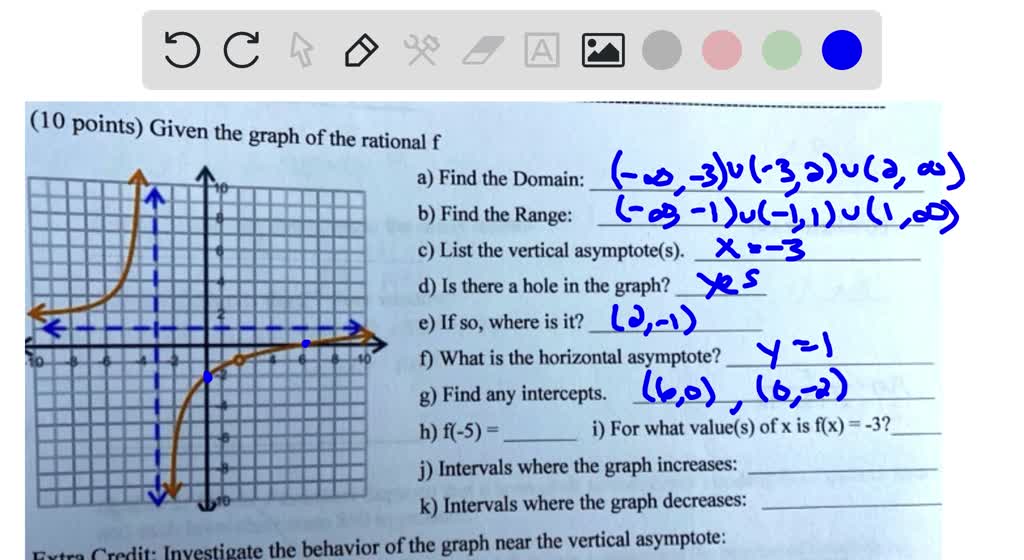
SOLVED: (10 points) Given- the graph of the rational f a) Find the Domain: b) Find the Range: c) List the vertical asymptote(s) d) Is there hole in the graph? e) If
The graph is made up of three parts. The left part is defined for all values of x between – 4 and – 2. The part in the center is defined on the interval x > 0 and x ≤ 4. The part on the right is defined for x > 6 and x ≤ 6. The domain is written as a union of three intervals as follows.
Source Image: numerade.com
Download Image
Parametric Equations | Mathematics, Learning and Technology
How To: Given the formula for a function, determine the domain and range. Exclude from the domain any input values that result in division by zero. Exclude from the domain any input values that have nonreal (or undefined) number outputs. Use the valid input values to determine the range of the output values.

Source Image: colleenyoung.org
Download Image
Teaching in Special Education: Domain and Range
Parametric Equations | Mathematics, Learning and Technology
Answer: This is a radical function. The domain of a radical function is any x value for which the radicand (the value under the radical sign) is not negative. That means x+5\geq0 x+ 5 ≥ 0, so x\geq−5 x ≥ −5 . Since the square root must always be positive or 0 0, \displaystyle \sqrt x+5\ge 0 x+5 ≥ 0.
Domain and Range of a Function SOLVED: (10 points) Given- the graph of the rational f a) Find the Domain: b) Find the Range: c) List the vertical asymptote(s) d) Is there hole in the graph? e) If
Identify Graphs of Basic Functions. We used the equation y = 2x − 3 y = 2 x − 3 and its graph as we developed the vertical line test. We said that the relation defined by the equation y = 2x − 3 y = 2 x − 3 is a function. We can write this as in function notation as f(x) = 2x − 3. f ( x) = 2 x − 3. It still means the same thing.